Die Größen der Technik

Jakob Steiner

Jacob Steiner ist ein Schweizer Bauernbub. Seine Eltern, Nikolaus Steiner und Anna Barbara Weber, betreiben eine kleine Landwirtschaft in Utzenstorf bei Solothurn im Kanton Basel und haben vor ihm schon drei Söhne und eine Tochter. Der kleine Jacob kommt am 18. März 1796 als letztes Kind zur Welt und wird von früher Jugend an von den Eltern als Hüterbub eingesetzt. Am Samstag darf mit dem Vater auf den Markt nach Solothurn mitkommen, wo er den Bauern die Marktrechnungen im Kopf vorrechnet und sich dadurch ein wenig Taschengeld verdient. Angeblich lernt er erst mit 14 Jahren Schreiben.

Er hört vom Institut von Heinrich Pestalozzi in Yverdon, am Südende des Lac de Neuchatel gelegen, und bricht 1814 gegen den Willen seiner Eltern dorthin auf, um nach anderthalb Jahren als Seminarist an dieser Schule selbst dort als Junglehrer für Mathematik zu unterrichten. Allerdings hat die Anstalt ihre Blütejahre bereits überschritten.

Diese Kreidezeichnung von Jacob Steiner hat Nikolaus Senns zwischen 1830 und 1840 angefertigt.

Die Mathematikhefte des Schülers Jacob Steiner sind erhalten, und so ist bekannt, dass er den ersten Unterricht in Planimetrie (Geometrie der Ebene) von einem Herrn Maurer erhält, der ihn zunächst in Dreiecken, dann in Vierecken und Fünfecken, später im pythagoräischen Lehrsatz unterweist, bis er von Fridolin Leuzinger abgelöst wird, der selbst in Heidelberg seinen mathematischen Schliff erhalten hat. Es geht weiter mit dem Kreis und geometrischen Verhältnislehren, und dann folgen ein Lehrgang in Stereometrie und ein algebraischer Unterricht, der jedoch dann abgebrochen wird. Steiner schreibt an einen Freund: „Denn sowie Formeln kommen, so bin ich blödsinnig.“

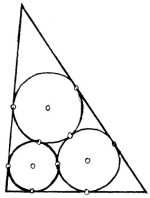
Steiners Lösung des Malfatti-Problems. Zusätzlich transferiert er diese Fragestellung auch in den Raum.

Die drei anschließenden Hefte über die Formenlehre scheinen jedoch bei Steiner so nachhaltig gewirkt zu haben, dass er eine seiner ersten eigenen Veröffentlichungen dieser Thematik widmet. Mechanik, ebene und sphärische Trigonometrie runden seine mathematische Ausbildung Anfang 1817 ab, und nun unterrichtet er selbst, bis er im Herbst 1818, wohl in Nachahmung seines Lehrers Leuzinger, nach Heidelberg geht, um dort wie auch dieser bei Franz Ferdinand Schweins zu hören. Allerdings geht die Überlieferung betreffend Steiners Auffassung von der Brillianz des Professors auseinander. Einerseits wird berichtet, dass Steiner Schweins in seinen gesammelten Werken als „genialen Verfasser eine Analysis und als ausgezeichneten Kombinatoriker“ hervorhebt, andererseits hinwiederum, dass „er später die dort vorgetragene Geometrie mit wenig schmeichelhaftem, dem Namen des Lehrenden entnommenen Beiworte bezeichnete.“ Am Schluss seiner Studien soll er sich mit Professor Schweins überworfen haben.

Nach seiner Promotion in Heidelberg geht Jacob Steiner als Institutslehrer am Friedrich-Werderschen Gymnasium nach Berlin, überwirft sich jedoch wegen seiner Kritik am dort verwendeten Mathematik-Lehrbuch bald mit seinen Vorgesetzten und quittiert den Schuldienst. Aber bereits 1822 ist er als der beste Privatlehrer in Mathematik so bekannt, dass auch der Gründer der Berliner Universität, Wilhelm von Humboldt, seinen Sohn bei ihm ausbilden lässt, was dem Bauernbub aus dem Berner Mittelland Zutritt nicht nur in deren Haus, sondern auch in deren Gesellschaft ermöglicht, hat sich doch die Familie Humboldt in der Zeit, als Wilhelm Gesandter in Rom war, länger in Bern aufgehalten. Zwar ist das schon gut 20 Jahr her, aber Caroline von Humboldt mischt nach wie vor gerne berndeutsche Ausdrücke in ihre Konversation.

Durch diese Kontakte erhält er eine Stelle am erst wenige Jahre zuvor durch Peter Christian Wilhelm Beuth gegründeten Berliner Gewerbeinstitut, was ihn wiederum in Bekanntschaft zu allen derzeit in Berlin befindlichen Mathematikern bringt. Zu dieser Zeit entfaltet Steiner auch eine ausgedehnte Publikationstätigkeit, insbesondere wie auch der norwegische Mathematiker Niels Henrik Abel im neuen Journal für die reine und angewandte Mathematik von August Leopold Crelle. Die drei Mathematiker werden im Berliner Volksmund „Adam mit seinen Söhnen Kain und Abel“ genannt, wofür wohl die Altersverteilung und der Name des Analytikers Abel Pate stehen, nicht jedoch das Verhältnis der beiden jüngeren zueinander. Zwar stirbt Abel früh, jedoch an Lungentuberkulose.

Steinersche Fläche. Die Graphik stammt von A13ean.

Steiner bearbeitet in erster Linie das in Deutschland relativ neue Gebiet der synthetischen Geometrie, die er durch seine Zweisprachigkeit in den renommierten französischen Journalen, insbesondere in Gergonnes Annales de mathématiques, nachlesen kann, wo Poncelet das von ihm erfundene „Prinzip der Dualität“ veröffentlicht und über seine „Théorie des polaires réciproques“ schreibt. In seinem Jahrzehnt als Lehrer an der Beuth´schen Gewerbeschule veröffentlicht Steiner auch zwei Lehrbücher, die seinen Ruf als hervorragender Geometer festigen. Es sind dies Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander, mit Berücksichtigung der Arbeiten neuer und alter Geometer über Porismen, Projections-Methoden, Geometrie der Lage, Transversalen, Dualität und Reciprocität, etc., erschienen in Berlin bei Fincke 1832, und Die geometrischen Konstruktionen, ausgeführt mittels einer geraden Linie und eines festen Kreises aus dem Jahre 1833. Diese beiden bleiben die einzigen Monographien von Steiner, der sonst nur noch in Zeitschriften publiziert. Die Systematische Entwicklung der Abhängigkeit geometrischer Gestalten von einander ist noch dazu nur der erste Teil eines auf fünf Bände angelegten Gesamtwerkes, zu dessen Weiterführung es nie gekommen ist. Die wesentlichsten Inhalte trägt er immer wieder in einer Hochschulvorlesung unter dem Titel Populäre Kegelschnitte vor. Posthum sind seine Vorlesungen von zwei seiner Schüler herausgegeben worden, und Kritiker freuen sich, dass diese Herausgabe nicht durch Steiner selbst erfolgt ist, sondern durch Geiser und Schröter, die sich um Anschaulichkeit bemüht haben. Denn Steiners geometrisches Glaubensbekenntnis huldigt der synthetischen Methode, im Gegensatz zur analytischen.

Die synthetische Geometrie sieht die Formen im Raum und imaginiert die Eigenschaften dieser Formen durch reine Vorstellungskraft. Diese überträgt man dann an geeigneter Stelle, was neue Eigenschaften ergibt, eine neue Vorstellung. Die analytische Geometrie hingegen ersetzt die Figuren durch Koordinaten und Parameter und überträgt das geometrische Problem auf eine rechnerische Ebene, löst es und macht dann eine „Rückübersetzung“ in die Sprache der Geometrie.

Steiner will die Abhängigkeit der Gestalten von einander aufdecken, und die Art und Weise, wie sie ihre Eigenschaften von den einfacheren Figuren zu den zusammengesetzten fortpflanzen, und ist nicht überrascht, dass die Ergebnisse sich im Nachhinein auch analytisch rechtfertigen lassen, ist aber der Ansicht, dass „die Analysis einem die Schlafkappe über den Kopf ziehe“ und man nicht sehr aufmerksam schauen müsse, wie er in einer Vorlesung äußert.

Über den Kontakt zum Mathematiker Carl Gustav Jacob Jacobi, der nach seiner Zeit als Privatdozent in Berlin eine Professorenstelle an der Universität in Königsberg antritt und dadurch Königsberg zu einem mathematischen Zentrum macht, erhält er 1833 dort ein Ehrendoktorat und wird ein Jahr später auf Veranlassung Wilhelms von Humboldt in die königlich preußische Akademie der Wissenschaften aufgenommen. Im selben Jahr wird an der Berliner Universität extra für ihn eine außerordentliche Professur für Geometrie eingerichtet, die es Steiner gestattet, sich von der zeitaufwendigen Schul-Lehre zurückzuziehen und neben seinen Vorlesungen mehr der Forschung zu widmen.

Steiner ist zwar eine Koryphäe auf seinem Gebiet, jedoch bereitet ihm das Rechnen mit numerischen und algebraischen Größen Schwierigkeiten, und Jacobi ist es, der ihm immer wieder bei der Fehlersuche hilft und „mittels eines verfluchten Judenkniffs“, wie Steiner sich auszudrücken beliebt, eine Lösung inert 5 Minuten hat, an der Steiner selbst stundenlang gescheitert ist. Im Gegensatz zu Steiner, der der Ansicht ist, aus Büchern könne jeder lernen, ein wahrer Mathematiker solle die Bücher in sich tragen, ist Jacobi, der zum Protestantismus konvertierte Sohn eines Vorstandsmitgliedes der jüdischen Gemeinde in Potsdam, sehr in der mathematischen Literatur bewandert. Er gibt Steiner zwei Sätze des römischen Mathematikers Pappus, die dieser nicht lösen kann, was diesen für längere Zeit sehr demütigt. Jacobi bewahrt Steiner auch vor der Peinlichkeit, mathematische Sätze zu veröffentlichen, die Poncelet bereits in Traité des propriétés projectives des figures niedergelegt hat. Steiner nähert sich nämlich, wie er selbst beschreibt einem mathematischen Problem an, indem er „nicht eher über eine Aufgabe oder über einen Gegenstand weiter nachliest, bevor er nicht selbst eine Auflösung oder Sätze darüber gefunden hat, um alsdann seine Resultate mit den schon vorliegenden zu vergleichen.“ Das führt natürlich zu Lösungen und Sätzen, die bereits existieren.

Jacob Steiner dürfte kein besonders angenehmer Zeitgenosse gewesen sein. In seinen ersten Jahren in Berlin wird er als „ungelenker Schweizer“ bezeichnet, und als er 1843 mit seinen Kollegen Jacobi, Dirichelet und Borchardt eine Reise nach Rom unternimmt, engagiert er den Schweizer Mathematiker Ludwig Schläfli als Dolmetsch und preist ihn seinen Reisegefährten an als „ländlichen Mathematiker bei Bern, für die Welt ein Esel, aber Sprachen lerne er wie ein Kinderspiel“, und bezeichnet ihn als „genialsten Tölpel, der ihm in der Welt vorgekommen sei“.

Allerdings entsteht mit Schläfli, der Steiners Größe anzuerkennen in jeder Lebenslage bereit ist, dann doch eine Freundschaft. Beide erwägen mehrfach eine gemeinsame Publikation, und mehrfach rechnet Schläfli nach, was Steiner gezeichnet hat. Auch unterstützt Steiner Schläflis Bemühungen, an der Universität Bern oder am neu gegründeten Zürcher Polytechnikum eine Professur zu erhalten, und setzt sich sehr dafür ein, dass dieser seine Abhandlungen an die maßgeblichen Stellen schickt, damit er in prominenten Journalen veröffentlicht wird und auch Ruhm und Ehre von seinem Schaffen davontragen kann, nicht nur Versicherungsmathematik für die Schweizer Nationalvorsichtskasse betreibt. Schlussendlich überwirft er sich aber doch noch mit Schläfli, der sich und seine zahlreichen Unterstützungen, über die ein dokumentierter Briefwechsel Aufschluss gibt, von Steiner nicht angemessen gewürdigt fühlt und den Kontakt einschlafen lässt. Auch Lexikoneinträge werfen Steiner unaufrichtiges Zitieren vor und zählen das zu seinem „ungewöhnlichen Verhalten“, das ihn in der wissenschaftlichen Welt Außenseiter bleiben lässt.

Portrait aus: Der Mathematiker Jacob Steiner von Utzenstorf. von J.H. Graf. 1897

Ab Mitte der 1850er Jahre geht es Steiner körperlich immer schlechter, so dass er zu mannigfachen Kuraufenthalten in verschiedenen Bädern gezwungen ist. Sein ohnehin nicht sehr gewinnendes Wesen wird immer missmutiger, mit den gleichaltrigen Fachkollegen sind die persönlichen Bindungen zerfallen, mit jüngeren verabsäumt er es Verbindungen zu knüpfen. Anders als viele, die im Ausland Karriere machen, kehrt Steiner immer wieder nach Bern und Utzenstorf zurück und verbringt dort regelmäßig seine Sommer oder ganze Jahre zur Wiederherstellung seiner Gesundheit, führt aber auch dort in einem Gasthof das Leben eines Sonderlings. Wegen seines beißenden Spotts wird er auch von der Dorfbevölkerung nicht besonders geschätzt. Er soll dem Schweizer Schriftsteller Jeremias Gotthelf, dessen Vater ab 1805 Pfarrer in Utzenstorf ist und mit dem er als Kind öfter gespielt hat, einige Beiträge zu seinen Volksdichtungen geliefert haben.

Jacob Steiner stirbt als Junggeselle am 1. April 1863 in der Berner Kramstraße 162, wo er ein Zimmer bewohnt, an der Wassersucht, und wird ohne viel Beteiligung am Berner Monbijou-Friedhof beigesetzt. Sein Grab ist bald vergessen, bis einige zwanzig Jahre später zwei junge Mathematiker die Grabstätte finden und ein ehemaliger Schüler Steiners einen Grabstein stiftet. Weil der Monbijou-Friedhof geschlossen werden sollte, finden sich Berner Mathematiker, die die sterblichen Reste von Jacob Steiner exhumieren und in ein vom Gemeinderat Bern zur Verfügung gestelltes Grab im Bremgartenfriedhof betten, gleichzeitig mit der Einweihung von Schläflis Denkmal, am 100. Geburtstag Steiners am 18. März 1896. Angelegentlich der Exhumierung wird Steiners Schädel vermessen – wohl eine Zeiterscheinung, wenn wir an die bald darauf folgende Rassenlehre denken, die ausgesprochen gefährliche Blüten getrieben hat. So erfahren wir, dass Steiners Schädel, wie übrigens die überwiegende Zahl der Bewohner des Berner Mittellandes, brachycephal und leptoprosop ist.

Allenthalben wird seine geometrische Vorstellungskraft und sein seltenes Kombinationsvermögen herausgestrichen, und gleichzeitig dem Bedauern Ausdruck verliehen, dass dieses Talent auf das enge Gebiet der Geometrie beschränkt ist. Aber dort streut ihm sein Schüler Geiser Rosen: „Wir haben in ihm den größten Geometer unseres Zeitalters besessen, auf dessen Schöpfungen noch künftige Jahrhunderte in Forschung und Lehre weiterbauen werden.“

Steiner pflegt auch persönliche Kontakte zu Mathematikern in Paris, namentlich zu „General Poncelet“, wie er Jean-Victor Poncelet zu nennen pflegt, weil dieser 1812 an Napoléons Russlandfeldzug teilgenommen hat, der selbst ein Schüler von Gaspard Monge ist und als Erfinder der modernen projektiven Geometrie gilt. 1854 wird Steiner durch diesen Kontakt zum korrespondierenden Mitglied der Pariser Académie des Sciences ernannt, wie auch bereits 1853 schon zu einem solchen der Accademia die lincei in Rom, die ja für die älteste noch heute existente Gelehrtengemeinschaft gilt.

Mehrere Phänomene sind nach Jacob Steiner bekannt:

• In der Mechanik der Steinersche Satz zur Berechnung des Trägheitsmoments von geometrischen Körpern, deren Schwerpunkt außerhalb der Drehachse liegt.
• Das Steinerbaumproblem gehört zur Optimierung und wird in der Logistik angewandt
• Die Steinersche Fläche ist eine Fläche vierten Grades, deren Tangentenebenen in zwei Kegelschnitten schneiden, und mit drei durch einen Punkt gehenden Doppelgeraden. Sie wird auch Römerfläche genannt, weil Steiner sie auf seiner Romreise 1843 gefunden hat.