Die Größen der Technik
<< zur NamenslistePierre-Simon Laplace
Pierre Simon Laplace wird im März 1749 in der Normandie als Sohn eines reichen Bauern geboren und soll auf Wunsch des Vaters eine geistliche Laufbahn einschlagen, weshalb er am Jesuiten-Kolleg in Caen Theologie und Philosophie studiert. Dort wird seine mathematische Fähigkeit erkannt, und er kommt mit 19 Jahren mit einem Empfehlungsschreiben nach Paris zu Jean-Baptiste le Rond d´Alembert, dem berühmtesten zeitgenössischen Mathematiker und Mitherausgeber der Encyclopédie, der ihn sehr fördert. Er verschafft ihm einen wenig fordernden Posten als Mathematiklehrer an der Pariser Militärschule, die ihm Zeit für seine weiteren Studien und Forschungen lässt. In Wahrheit wissen wir nur wenig über seine Herkunft und Jugend, weil er alle Brücken zu Familie und frühen Förderern und Gönnern abgebrochen hat.
Laplace, von früher Jugend an seiner Karriere bastelnd, bewirbt sich ab 1771 um seine Aufnahme in die Pariser Académie de Sciences, wo ihm jedoch ältere Mitbewerber vorgezogen werden. Daraufhin schreibt sein Förderer d´Alembert einen Brief an Lagrange, der sich zu dieser Zeit in Berlin aufhält, um Laplace wenigstens in der Preußischen Akademie der Wissenschaften unterzubringen, was sich jedoch wegen dessen Aufnahme als Adjunkter an der Académie Francaise erübrigt. 1784 wird Laplace dann auch ordentliches Mitglied der Académie des Sciences.
Weiterhin als Wissenschafter tätig, wird Laplace 1784 Prüfer für die Absolventen der Artellerie-Klasse der königlichen Militärschule, deren Unterricht in erster Linie aus Hydrostatik, Differenzial- und Integralrechnungen besteht, ergänzt durch Staatsrecht und Befestigungskunde. Neben den vielen Söhnen aus den besten Häusern Frankreichs ist 1785 auch der 16jährige Napoléon Bonaparte einer seiner Prüflinge. Gleichzeitig wird Laplace ordentliches Mitglied an der Académie des Sciences und 1792, im Jahr der Abschaffung der Monarchie, Mitglied des Komitees für Maße und Gewichte.
Laplace wird im Laufe seines Lebens Mitglied in allen wichtigen europäischen wissenschaftlichen Akademien.

Laplaces Forschungen werden während der Französischen Revolution nur in der Zeit der Schreckensherrschaft der Jakobiner unter Maximilien de Robespierre unterbrochen. Nach dessen Guillotinierung am 10. Thermidor II (das ist der 28. Juli 1794) kehrt Laplace wieder aus Melun nach Paris zurück und nimmt seine Arbeit im Komitee für Maße und Gewichte wieder auf. Er wird einer der beiden Endprüfer in der neu gegründeten ersten technischen Hochschule der Welt, der Ecole polytechnique, und ist Gründungsmitglied und Vizepräsident, Monate drauf schon Präsident des „Institut de France“, der Dachorganisation aller wissenschaftlichen französischen Akademien. Des Weiteren ist er Leiter des Pariser Observatoriums.
Laplace, immer an der Karriere arbeitend und sich den jeweiligen Machthabern gut anpassend, empfiehlt sich seinem ehemaligen Prüfling Napoléon Bonaparte so weit, dass ihn dieser nach seinem Staatsstreich am 18. Brumaire VIII (das entspricht dem 9. November 1799 im gregorianischen Kalender) zum Innenminister macht, nach 6 Wochen jedoch schon gegen seinen Bruder Lucien austauscht, weil jener „den Geist des unendlich Kleinen in die Verwaltung mitbrachte“. Der Wissenschafter hingegen wird zum Mitglied des Senats gemacht, wo er wenig Schaden anrichten kann, und 1804 zum Grafen erhoben.

Gemeinsam mit seinem Nachbarn, dem Chemiker Berthollet, gründet er in ihrem Wohnort südlich von Paris die Société d´Arcueil, eine wissenschaftliche Gesellschaft zur Förderung junger Talente. Auch Alexander von Humboldt gehört dieser Gesellschaft an.
Nach der Verbannung Napoléons nach Elba stimmt Laplace für die Wiedereinsetzung der Bourbonen und nimmt auch während der Herrschaft der 100 Tage kein politisches Amt an, wofür ihn Louis XVIII 1815 zu einem der 12 Pairs de France und 1817 zum Marquis ernennt. 1816 legt Laplace seine Arbeit an der Ecole polytechnique nieder und wird Inhaber des Sitzes Nr. 8 der 40 Unsterblichen der Académie française.
Er stirbt 1827 und wird trotz seiner großen wissenschaftlichen Verdienste nicht im Pantheon, sondern auf einem Pariser Friedhof beigesetzt. Alexander von Humboldt war bei der Beerdigung anwesend. Er ist als Nr. 9 unter den 72 Namen auf dem Eiffelturm verewigt.
Laplace ist mit Antoine Lavoisier gut befreundet. Im Jahre 1782 arbeitet Alessandro Volta aus Como, Professor für Experimentalphysik in Pavia, 4 Monate mit den beiden.
1788 heiratet er mit Marie-Charlotte de Courty de Romanges eine wesentlich jüngere Frau des französischen Adels und hat mit ihr zwei Kinder. Alle heutigen Nachfahren von Laplace stammen von der Tochter seiner Tochter ab und tragen daher nicht seinen Namen.
Pierre Simon Laplace wird zu Lebzeiten als französischer Newton gehandelt (der genau 100 Jahre vor ihm stirbt.)
Sein wichtigstes Forschungsgebiet ist die Himmelsmechanik, mit der er sich in seinen letzten 30 Jahren befasst. Hier präsentiert er, dem Zeitgeist entsprechend, sein Wissen einmal als nichtmathematische Einführung in die Himmelsmechanik, für die breite Masse quasi, und dann als mathematisch sehr anspruchsvolles ebenfalls fünfbändiges Werk unter dem Titel „Traité de Mécanique Céleste“, in dem er einen rechnerischen Beweis für die Stabilität der Planetenbahnen erbringt und die Existenz Schwarzer Löcher vorhersagt. Dieses Buch, obwohl schwer zu lesen, wird für lange Zeit Pflichtlektüre für angehende Astronomen.
Laplace beschäftigt sich Zeit seines Lebens mit der Wahrscheinlichkeitsrechnung, weil das für ihn der Ausweg war, Ergebnisse abzuschätzen, ohne genauere Kenntnisse über ihr Zustandekommen zu haben. Denn obwohl Laplace sich mehr als Physiker denn als Mathematiker versteht, weil ihm die Mathematik immer nur als Mittel zum Zweck dient, haben seine mathematischen Verfahren auch heute noch große Bedeutung.
Die Laplace-Formel gibt eine sehr wichtige mathematische Beziehung in der Stochastik wieder: Besitzen alle Ergebnisse eines Zufallsexperimentes die gleiche Wahrscheinlichkeit, so gilt für die Wahrscheinlichkeit P(A) eines Ereignisses A:
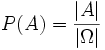
Die Laplace-Transformation und deren Inversion sind ausgesprochen wirkungsvolle Verfahren zur Lösung vieler Problemstellungen der mathematischen Physik und der theoretischen Elektrotechnik, welche mathematisch durch lineare Anfangs- und Randwertprobleme beschrieben werden. Die wichtigste Eigenschaft der Laplace-Transformation besteht darin, dass der Differentiation und Integration im reellen Originalbereich einfache algebraische Operationen im Bildbereich entsprechen. Bei vielen Anfangs- und Randwertproblemen spielt der Zeitbereich die Rolle des reellen Originalbereiches und der Frequenzbereich oder Spektralbereich diejenige des komplexen Bildbereiches. In Maschinenbau und Elektrotechnik, speziell in der Regelungstechnik, spielt die Laplace-Transformation eine große Rolle. So können beispielsweise Stabilität, Schwingungsverhalten und Schnelligkeit sowohl von Regelstrecken als auch von geschlossenen Regelkreisen viel einfacher analysiert werden.
Bedeutung der Laplace-Gleichung in der Physik: In der Elektrotstatik genügt das elektrische Potential im ladungsfreien Raum der Laplace-Gleichung. Sind eine geometrische Leiteranordnung sowie das Potential der Leiter gegeben, so liegen Dirichlet-Randbedingungen vor (sofern die Leiter kein beschränktes Gebiet umschließen, nimmt man als weitere Randbedingung an, dass das Potential im Unendlichen gegen null geht). Dann gibt es genau eine Lösung der Laplace-Gleichung, das elektrostatische Potential. Beispielsweise ist das Potential in einem Faradayschen Käfig konstant.
Der Laplace-Operator ist der Differentialoperator in der Laplace-Gleichung für das elektrostatische Potential im Vakuum außerhalb leitender, geladener Körper und in der Poisson-Gleichung für das Potential einer zeitunabhängigen Ladungsdichte. Zusammen mit anderen Ableitungen tritt er in der Wellengleichung und der Diffusionsgleichung auf. Große Bedeutung hat er auch für Berechnungen in einem Schwerefeld.
Der Laplace´sche Dämon ist ein Begriff aus einem Grenzgebiet der Philosophie und der Physik und dient heute nur noch dazu, den Begriff Determinismus zu veranschaulichen, war zu seiner Zeit aber ein Aufreger in der philosophischen Landschaft. Laplace befindet 1814 in seinem philosophischen Versuch über die Wahrscheinlichkeiten, dass man quasi eine Weltformel aufstellen könnte, wenn man alle Naturgesetze und alle Initialbedingungen kennt. Von dort aus kann man alle vorangegangen und alle kommenden Zustände berechnen.
„Wir müssen also den gegenwärtigen Zustand des Universums als Folge eines früheren Zustandes ansehen und als Ursache des Zustandes, der danach kommt. Eine Intelligenz (entspricht „Dämon“), die in einem gegebenen Augenblick alle Kräfte kennte, mit denen die Welt begabt ist, und die gegenwärtige Lage der Gebilde, die sie zusammensetzen, und die überdies umfassend genug wäre, diese Kenntnisse der Analyse zu unterwerfen, würde in der gleichen Formel die Bewegungen der größten Himmelskörper und die des leichtesten Atoms einbegreifen. Nichts wäre für sie ungewiss, Zukunft und Vergangenheit lägen klar vor ihren Augen.“
Nach dem heutigen Stand der Wissenschaft stehen dieser Aussicht auf den Weltenlauf mehrere Widrigkeiten gegenüber: die Unlösbarkeit des Dreikörperproblems, die Beschränktheit der Lichtgeschwindigkeit, die System
